タップについて

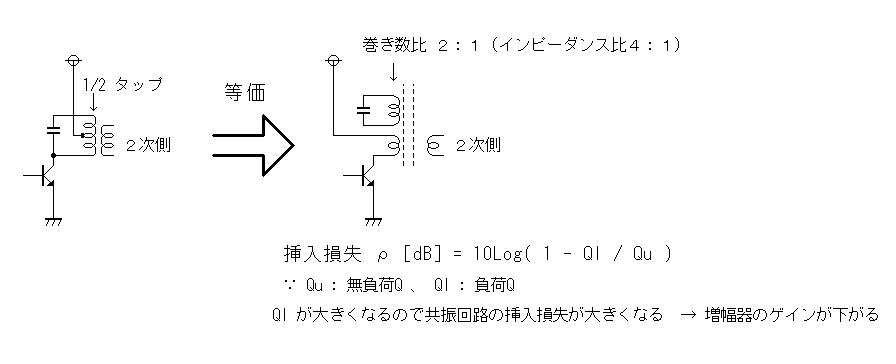
タップはFCZコイルにならって１次巻き線の半分の巻数位置から出しています。
半分の位置にしておけば、コイルの足ピン１番と３番は２番ピン（タップのピン）に対して対照となり、どちらに接続しても同じになるので、接続の間違いを防げます。

タップを持ったコイルは、１次と２次の巻き線を共有したトランスと同じですから、結合係数は１に近く、従ってインピーダンス比がほぼ４：１のトランスと見ることが出来ます。

タップを使用すると負荷インピーダンスがステップアップされて同調回路の負荷Ｑ ( Ql とします）が上がり、同調がよりシャープになるとともに、同調回路の挿入損失が増えて増幅器のゲインが低下しますので、異常発振の防止になります。
(タップをトランジスタのコレクタに接続して、同調回路のホットエンドを電源に接続しても動作は同じです。)







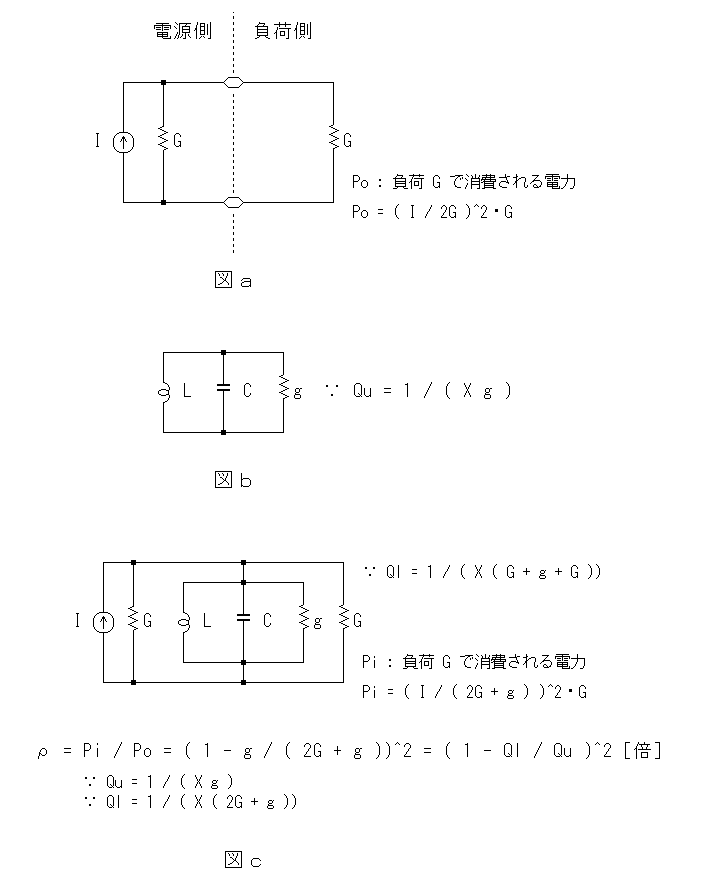
ここで、下図 ａ のようなコンダクタンスＧの電流源（信号源）に負荷コンダクタンスＧが接続されている回路（従ってマッチングがとれているので負荷コンダクタンスＧには最大の電力 Po が供給されている）に並列同調回路を挿入する場合を考えて見ます。（コンダクタンスは抵抗の逆数 1/R です。計算を簡単にするため、ここではコンダクタンスで考えます。)

このとき、負荷コンダクタンスに供給される電力を Po とすると

Po = ( I / G )^2・G

この図ａの回路に並列同調回路 図ｂ が接続されたときに負荷コンダクタンスＧ に供給される電力を Pi とすると

Pi = ( I / ( G + g + G ))^2・G

従って、並列同調回路を接続したときの挿入損失ρ[ 倍 ] は

ρ = Pi /Po = ( G / ( G + g + G ）)^2

となります。

ここで、無負荷Ｑを Qu　、　負荷Ｑを Ql とすると　（X は共振しているときのコイルまたはコンデンサのリアクタンス)

Qu = 1 / ( X g )
Ql = 1 / ( X ( G + g + G )

ですから、ρの式を Qu 、 Ql で表すと

ρ = ( １-　Ql / Qu )^2 　[ 倍 ]

となり、Ql が大きいほど挿入損失ρが低下します。