---

本機は、バンドギャップリファレンスを利用して高精度な電圧を発生するシャントレギュレータ IC テキサスインスツルメンツ社の LM4040-4.1 を使用してます。
私は、以前、秋月電子で購入しましたが、今は DigiKey , Mouser , RSコンポーネンツなどで取り扱いがあるようです。
このシャントレギュレータ IC は温度の影響をほとんど受けず、0.1% の精度で 4.096 V を発生しますので、テスターなどの校正に使うことができます。


製作は、いたって簡単で ユニバーサル基板の切れ端に LM4040 を実装して基板ごと端子へハンダづけしています。

内部写真

ユニバーサル基板の切れ端に実装

回路図は、ここをクリック　して下さい。

---

バンドギャップリファレンスについて

鉄などの導体に電流を流す場合と違い、PN接合などの半導体に電流を流すためには、ある程度の電圧を印可して価電子帯の電子をその間にある禁則帯を飛び越えて伝導帯にまで叩き出す必要があります。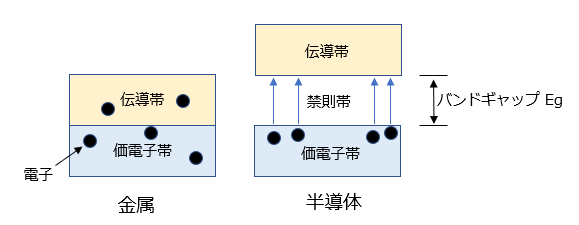



この価電子帯から伝導帯へ移動するためのエネルギーをバンドギャップ Eg といい、単位は エレクトロンボルト [eV] です。
絶対温度 0 °K においてシリコンの PN接合の Eg は 約 1.17 [eV] です。
1 [eV] は、1[V] の電圧を印可したときに電子に与えられるエネルギーなので、絶対温度 0 °K においてシリコンの PN接合に電流を流すためには 1.17 [V] の順方向電圧 Ev を印可する必要があります。

また、シリコンの PN接合の順方向電圧 Vf は約 -1.8 [mV/℃] の負の温度係数を持っており、

        Vf =  Ev - 1.8 E-03 ・T        T ：絶対温度 °K

で表わされます。従って常温付近では Vf = 0.6 [V] 程度になります。

一方、全く均一のシリコン PN接合があったとしても電流密度によって Vf は異なってきます。
異なる Vf の片方を Vf ' とすると Vf は負の温度係数を持ちますが、(Vf - Vf ') は正の温度係数を持ちます。
これを利用して

        Vo = Vf + m (Vf - Vf ')

となる回路を構成し、ｍ の値を調整して Vf の負の温度係数を打ち消せば、常温においてシリコン PN 接合の Ev ＝ 1.17 [V]を再現することができます。
このような回路をバンドギャップリファレンスと呼び、1971年に Rober. J. Wilder によって発明された ワイルダーのバンドギャップリファレンス回路が有名です。


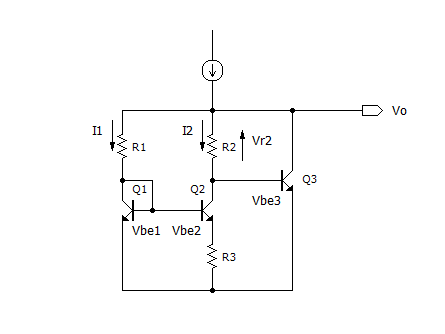
              Wilder のバンドギャップリファレンス回路

ワイルダーのバンドギャップリファレンス回路の動作

ワイルダーのバンドギャップリファレンス回路の動作を説明します。

各トランジスタ Q1, Q2, Q3 は均一の PN接合で出来ているものとし、また計算を簡単にするため、ここでは各トランジスタのベース電流はゼロとします。


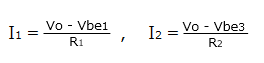
均一の PN接合なので Vbe1 と Vbe3 が等しいとすると


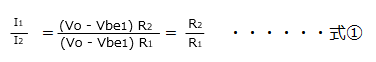
半導体の電気的なふるまいは、よく熱電圧 Vt を用いて説明されます。
熱電圧は絶対温度に比例し、下記の式で現されます。常温では Vt = 約 26 [mV] となります。

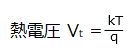
            k：ボルツマン定数 1.38E-23
            q：素電荷 1.60E-19   単位はクーロン [C]

PN接合に流れる電流については Shockley のダイオード方程式

によって表わされます。
ここで Is は逆方向飽和電流で PN接合に逆方向電圧を印可したときの漏れ電流に相当し、PN接合に印可される電圧 Vbe が負電圧のとき電流 I は、Is に近づきます。
Is はゲルマニュームダイオードなどでは比較的大きな値ですが、 IC 内部の PN接合などでは 1E-15 [A] など非常に小さい値となります。

Shockley のダイオード方程式を変形して


I >> Is なので


また

これは２つの Vbe の差なので温度係数は正となる要素です。

この式に式②を代入すると

さらに


となるのでリファレンス電圧 Vo は


Vt = kT / q なので


Vo の温度係数をゼロにすればよいので、先ず温度係数を求めるために温度 T で微分します。


式①を式③に代入すると


温度係数を表している式④の第１項（負の温度係数）と第２項目（正の温度係数）が打ち消しあえばよいので






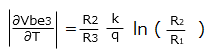
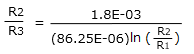
R2 と R1 の比が 10 : 1 とすると

R2 /R3 = 9.06

∴ R2 : R1 = 10 : 1 のとき、R2 : R3 = 9.06 : 1  の抵抗比にすると温度係数ゼロのリファレンス電圧（バンドギャップリファレンス）
   が得られることになります。
   例えば、R2 = 10 [kΩ]、R1 = 1 [kΩ] としたとき  R3 = 1.1 [kΩ] となりますが、理論的な動作はあくまで抵抗の比だけで決定され、
　抵抗の絶対値には依存しませんので、比率だけ守れば他の抵抗値でもＯＫです。